이 글은 하나의 저항 센서와 아날로그 대 디지털(analog-to-digital) 데이터 수집 시스템을 포함하고 있는 간단한 시그널 체인조차도 유효한 측정이 이루어지기 전에 처리해야 할 여러 가지 복잡한 요소들에 초점을 맞추고 있다.

글 | 카난 사다시밤(Kannan Sadasivam), qvs@cypress.com
애플리케이션 엔지니어
     사친 굽타(Sachin Gupta), sgup@cypress.com
     수석 애플리케이션 엔지니어
     싸이프레스 세미컨덕터(Cypress Semiconductor)

아날로그 양(analog quantity)의 측정을 위한 시그널 체인(signal chain)은 일반적으로 디자인 엔지니어들이 가장 어려워하는 도전과제이기도 하다. 하나의 저항 센서와 아날로그 대 디지털 데이터 수집 시스템이 있는 간단한 시그널 체인조차도 유효한 측정이 이루어지기 전에 처리해야 할 여러 가지 복잡한 요소들을 포함하고 있다.



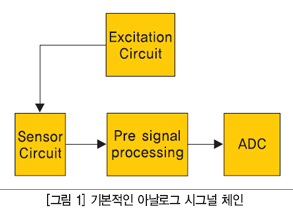
이러한 요소들은 시스템이 여러 센서와 동작할 때 관리하기가 훨씬 더 복잡하다. 이 글은 다양한 종류의 저항 센서와 함께 개발자가 정확한 측정을 위해 해결해야할 여러 가지 문제를 설명한다. 추상적인 수준에서, 저항 센서를 이용하는 모든 시스템에서 아날로그 시그널 체인은 그림 1에 나타낸 것과 다소 유사할 것이다.
모든 시그널 체인이 블록 수준에서 동일한 것처럼 보이지만, 각각의 블록에 대한 매개변수는 여러 가지 요소에 따라 다르다. 이러한 요소들에서 가장 중요하게 고려해야할 것은 물리적 수량에서 단위의 변화, 측정 시스템으로부터 센서의 거리(즉, 와이어 저항으로 인한 측정 오차), 시스템에 요구되는 정확성, 간섭의 유형, 필요한 정밀도를 위해 센서에 걸리는 저항의 변화이다(그로 인한 전압의 변화).
이러한 요소들은 필요한 여기(excitation)의 형태, 센서가 측정 회로에 연결되어야 하는 방식, 전처리(preprocessing) 회로 및 ADC에 필요한 이득(gain), 필터의 차단 주파수(cut-off frequency)를 비롯해 필요한 필터 유형, 해상도 및 ADC의 입력 범위 등을 결정한다.
서미스터(thermistor)로 시작하여 이것들을 이용하는 동안 여러 가지 센서 및 아날로그 시그널 체인에 관련된 주요 제약을 살펴보자. 서미스터는 온도 범위에 따라 극심한 비선형적인 특성을 나타낸다. 온도에 따른 저항의 변화는 다음과 같이 복잡한 비선형 함수이다:

  

여기서 T는 온도, R은 저항이다. A, B, C는 서미스터의 특정 상수이다. 방정식의 계산의 복잡성으로 인하여, 마이크로컨트롤러에서 구현하는 것이 적당하지 않을 수 있다. 따라서 이러한 계산을 구현하는 일반적인 방법은 저항과 해당 온도 값에 대한 룩업 테이블(lookup table)을 이용하는 것이다. 그리고 나서, 온도는 구간 연산(piece-wise arithmetic)을 사용하여 계산된다. 이득 변화와 오프셋으로 인하여 측정에 오차가 있을 수 있지만, 이러한 오차는 서미스터 기반 온도 센서의 정밀도 요건에는 극히 미미한 것이다. 이득 변화와 오프셋은 이 글 후반부의 RTD 부분에서 설명할 것이다.



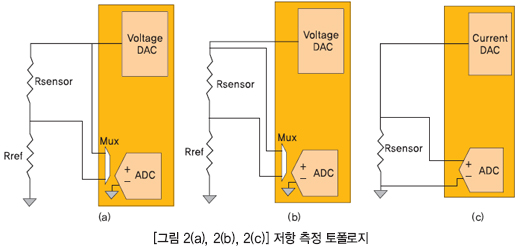
저항 측정을 고려하면, 그림 2에서 보는 바와 같이 여러 가지 직접 측정 방법이 있을 수 있다.
그림 2(a)에 나타낸 토폴로지는 저항 분할기(resistor divider)를 자극하기 위해 전압 DAC를 이용한다. 회로에 있는 저항 중 하나는 센서 자체이며 또 다른 저항은 알려진 값의 레퍼런스 저항이다. 이러한 토폴로지는 작동은 하지만, 단일 종단형(single-ended) 측정은 몇 가지 단점을 가지고 있다. 이러한 단점 중 하나는 오프셋을 초래할 센서 부근의 Vss와 ADC까지의 실제 내부 Vss 간의 접지 편이(ground shift)이다.
한편, 그림 2(b)에서 보는 바와 같이, ADC를 위한 -ve 입력이 저항 부근에 연결될 때 아날로그 접지와 ADC의 접지는 둘 다 같다. 차동 라인은 센서까지 서로 가까이 실행될 것이기 때문에, 어느 하나의 픽업(pick up)은 다른 것에 복제될 것이다. 차동 측정 구조를 이용하여 측정할 때, 이러한 시그널은 공통 모드 시그널이기 때문에 제거된다. 이러한 다이어그램에서 기타 유의할 점은 Rsensor에 걸린 전압을 측정하는 동안 +ve 입력이 센서 가까이에 연결된다는 것이다. 이는 와이어 저항으로 인해 측정에 오차가 없다는 것을 보증하는 것이다.
그림 2(c)는 센서를 자극하기 위해 전류 DAC를 이용하는 토폴로지를 보여주고 있다. 센서를 통해 측정된 전압은 저항의 정확한 측정치를 제공한다. 전류 여기(current excitation)는 필요한 외부 부품의 수량 측면에서 최상의 토폴로지이며, 어떠한 레퍼런스 저항도 필요 없다. 그러나 이득 오차에 대한 시스템을 보정하기 위해 외부 저항이 필요하다. 이러한 애플리케이션을 위해서는 매우 높은 정밀도가 필요 없으며 이득 오차를 보상하지 않아도 되기 때문에, 추가적인 레퍼런스 저항은 필요 없다.

저항 온도계
저항 온도계(Resistance Temperature Detectors, RTD)는 0 ℃에서 100 Ω의 저항을 가지며, 1 ℃의 온도 변화가 0.385 Ω의 저항 변화를 일으킨다. RTD는 낮은 저항을 갖기 때문에, 선간 저항(wire resistance)의 영향이 정확성에 중요한 역할을 한다. RTD로 온도를 측정하기 위해서는 정전류를 흘려서 온도에 따라 변화하는 저항값에 걸리는 전압을 측정한다. RTD에 걸리는 전압은 측정 시스템에서 RTD까지 병렬로 동작하는 와이어의 수를 기반으로 3-wire 방식이나 4-wire 방식을 이용하여 측정할 수 있다. RTD가 측정 시스템으로부터 떨어져 설치되므로 일반적으로 와이어 비용을 감안하여 3-wire 측정 방식이 선호되고 있다. 그림 3은 3-wire 측정 방식을 통해 연결된 RTD의 다이어그램이다.



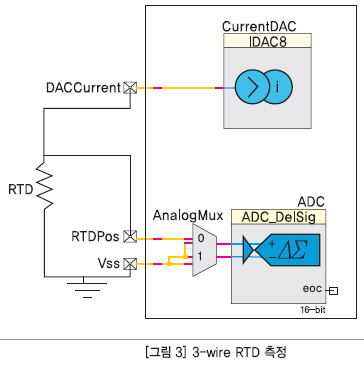
그림 3에서 전압이 첫 번째 채널에서 측정될 때, 이는 단지 RTD에 걸리는 전압만은 아니다. 사실, 이것은 RTD와 IDAC 및 RTD 간의 선간 저항을 통해 측정된 전압 강하이다. 선간 저항으로 인한 오차는 여러 가지 방식으로 처리할 수 있다. 그 한 가지 방법은 수동으로 와이어의 저항을 측정하고 그것을 상수로 저장하는 것이다. 매번 측정이 이루어지는 이런 저항은 공제될 수 있다. 또 다른 방법은 RTD의 양 단자(positive terminal)와 DAC의 출력 핀 사이의 전압 강하를 측정하는 것이다. 와이어가 같은 사양이라면, 이 와이어는 동일한 저항을 가질 것이며 이전 단계에서 측정된 전압은 센서를 통해 측정된 전압으로부터 감해질 수 있다. 그러나 와이어가 대칭이 아니라면, 일부 오차가 있을 수 있다. 또한 이 방법은 ADC 입력에 DAC의 출력 핀을 연결하기 위해 하나의 핀을 추가적으로 사용하게 될 것이다.



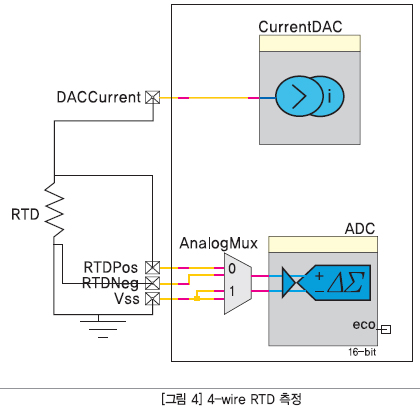
정밀한 측정을 위해서는 그림 4에서 보는 것처럼 4-wire 구성이 선호된다. negative 및 positive inputs 모두 RTD 가까이에 연결되며, 그로 인해 와이어 저항으로 인한 오차를 제거한다. RTD를 위한 시그널 체인을 설계하는 동안 체인의 입력 임피던스는 입력 전류를 유지하기 위해 아주 높아야 한다. ADC가 낮은 입력 임피던스를 가지고 있을 경우, 시그널은 ADC에 연결하기 전 버퍼에 공급된다.
앞서 언급한 것처럼, 온도 변화가 있게 되는 시스템에는 오프셋이 있을 것이다. 온도와 낮은 주파수 노이즈를 가진 offset/offset drift는 CDS (Correlated Double Sampling)를 이용하여 없앨 수 있다. CDS로 먼저 zero referenced offset이 측정되며, 이후 센서를 통한 전압이 측정된다. 그림 3과 4에서 zero referenced 시그널을 측정하기 위해 ADC는 채널 1에 연결된다. 센서를 통해 전압이 측정될 때 실제 열전대 전압, 오프셋, 그리고 노이즈가 포함될 것이다(방정식 1). 그림 3, 4에서 이는 채널 0에서 측정된 전압이다.

VR_Signal = VRTD + VN + Voffset ……(1)

제로 레퍼런스 리딩은 방정식 2에 의해 주어진다.

VZero_Ref = VN + Voffset………………(2)

현재의 제로 레퍼런스 측정과 관련하여 이전 제로 레퍼런스 샘플은 방정식 3에 의해 주어진다.
VZero_ref_Prev = (VN + Voffset)*Z-1… (3)

센서를 통한 현재의 전압 측정과 이전 제로 레퍼런스 시그널 간의 차이는 방정식 4에 의해 주어진다.

Vsignal = (VRTD + VN + Voffset) - (VN + Voffset)*Z-1………(4)

Vsignal = VRTD - (VN + Voffset)*(1-1/Z)…………………(5)

오프셋은 순차 샘플을 위해 매우 일정하므로, 방정식 5는 방정식 6이 될 것이다.

Vsignal = VRTD - VN*(1-1/Z)………(6)

이중선형 변환을 이용하여, T가 1/fsample인 Z = (1 + sT/2)/(1-sT)로 방정식 6은 방정식 7로 작성될 수 있다.

Vsignal = VRTD -VN*(2s/(s+ 2fsample) …(7)

방정식 7을 분석할 경우, 이는 high pass response이다. 반면, ADC는 low pass response를 가지며, 이는 시스템의 전반적인 노이즈를 줄이는 데 도움이 된다. 아울러, 그림 4에 나타낸 토폴로지를 보면, 시스템의 정확성은 전적으로 IDAC의 정확성에 달려있다는 것이 분명하다. 만일 IDAC가 5%까지 벗어나면, 계산 또한 5%까지 벗어날 것이다. 이는 측정에서의 이득 오차 조건이지 대부분의 시스템에 허용되는 것은 아니다. 첫 번째 이유인 ADC와 그 레퍼런스 정확성뿐 아니라, 이득 오차에 대한 또 다른 인자들이 있다. ADC가 단 1%의 정확한 레퍼런스를 가졌다면, 모든 측정은 이 1% 이득 오차에서 ADC suffer를 이용하여 만들어진다. 우리가 여기서 온도를 측정함에 따라 drift 문제는 훨씬 더 심도 있는 문제를 일으킬 수 있다.



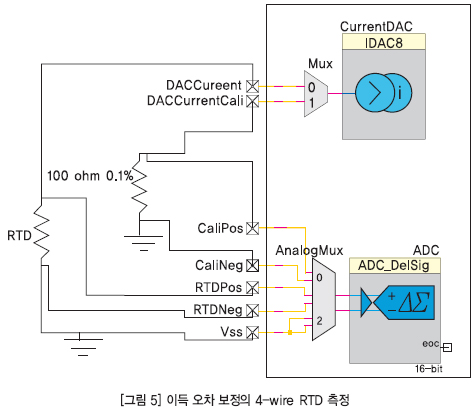
이러한 여러 가지 이득 오차의 영향을 피하기 위한 최선의 방법은 보다 정확한 매개변수에 대한 모든 측정을 참고하는 것이다. 0.1%의 정확한 저항은 이러한 목적을 위해 이용할 수 있다. 그림 5는 보정 저항이 연결된 토폴로지를 보여주고 있다.
전류는 먼저 레퍼런스 저항을 통해 전달되고 전압이 측정된다. 그로 인해 저항의 측정값을 제공한다. 이러한 측정은 앞서 논의한 이득 오차를 일으킬 경향이 있다. 그러나 다음 단계에서 같은 전류가 RTD를 통해 통과되며 이를 통해 전압이 같은 설정을 이용하여 측정된다. 두 ADC 측정 비율은 RTD의 저항 측정이 레퍼런스 저항에 관해 만들어지기 때문에, 어떠한 이득 오차도 없애준다. 시스템의 정확성은 현재 사용된 레퍼런스 저항의 정확성/허용오차를 기반으로 한다.

mVs에서 측정을 위한 고려사항
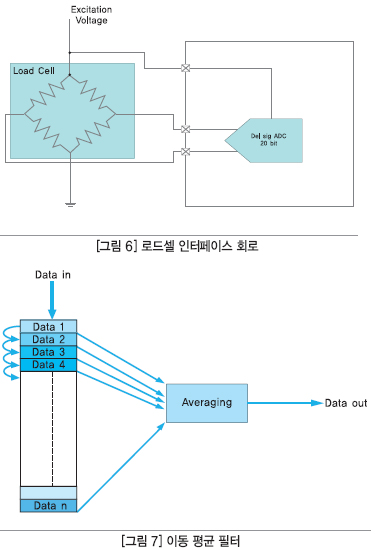
지금까지 우리는 측정 범위가 일반적으로 전압 범위에 있는 일반적인 고정밀 시스템에서의 정밀 아날로그 측정을 하기 위한 당면문제들을 논의했다. mVs에서 측정 범위를 가진 시스템들이 있는데, 이들 시스템은 설계자를 위한 완전히 새로운 도전과제를 제기한다. 이와 같은 시스템의 좋은 사례가 로드셀(load cell)이다. 로드셀은 물리적인 힘을 전기신호로 변환시켜주는 센서로 체중 측정을 위한 디지털 체중계에 일반적으로 사용된다. 전형적인 로드셀은 휘스톤 브리지(whetstone bridge) 네트워크에 4개의 저항이 배열된다. 이 센서는 전압을 이용한 두 개의 여기 단자에서 여기 되며, 센서에 적용된 힘을 기반으로 한 작은 전압은 측정 단자에서 설정된다. 로드셀의 출력 전압 범위는 일반적으로 1 V 여기 전압에 대한 출력 범위인 mV/V로 지정된다. 최대 10 kg의 무게를 측정하는 2 mV/V 로드셀의 사례를 들어보자. 사용자가 5 V 입력을 이용하여 이것을 여기하는 경우, 총 출력 전압 범위는 딱 10 mV이다. 이는 로드셀이 10 kg의 힘을 경험할 때조차도 출력은 딱 10 mV 일 것이라는 것을 의미한다. 이러한 10 mV 범위에서 16비트의 정밀도에 가깝게 결정하려는 것은 우리가 이러한 입력 범위에 맞게 ADC 범위를 줄여야 할 필요가 있음을 의미하는 것이다.
가장 흔히 사용되는 방식은 ADC 범위에 맞게 입력을 증폭하는 이득 스테이지(gain stage)를 구현하는 것이다. 이로 인해 보다 더 작은 범위 내에서 더 많은 비트를 해결한다. 예를 들어, 일반적으로 0+/- 1 V 범위를 가진 ADC를 이용하여 앞서 논의된 것처럼 10 mV의 측정 범위를 가지기 위해서 사용자는 증폭기를 기반으로 한 이득 스테이지를 이용하여 시그널에서 거의 100배의 이득을 취할 수 있다.
ADC를 1 V의 동적 범위로 측정할 때 최저 전압의 20-bit ADC는 1 uV를 볼 것이다. 이득 스테이지가 범위를 증가시키기 위해 사용될 때 이득 스테이지는 노이즈를 증폭시키며, ADC 측정에 영향을 끼칠 만큼 눈에 띄게 만들어준다. 이러한 노이즈는 ADC가 이득 설정에서 제공할 수 있는 가용 비트의 수에 영향을 준다. 따라서 하나는 필요한 이득 설정에서 최적의 해법을 주는 ADC를 선택해야만 한다.
보통 로드셀의 출력을 측정하기 위해 사용하는 ADC는 Delta Sigma (DelSig) ADC이며, 저역 통과(low pass) 필터이다. 싸이프레스 PSoC3과 PSoC5 디바이스에 있는 것과 같이 일부 DelSig ADC는 Delta Sigma 변조기 자체에서 이득을 추가하기 위한 기능을 제공한다. 이 경우 ADC 상의 두 개의 이득 효과는 0+/- 1.024 V에서 0+/-0.512 V까지 ADC의 입력 범위의 변화를 가져올 것이다. 따라서 우리는 ADC 변조기 자체에서 더 높은 이득을 달성할 수 있다. 또한 이렇게 하는데 있어서 중복 장점이 있다. ADC의 변조기에서 이득을 증가시킴에 따라 ADC의 대역폭은 줄어들기 시작한다. 이는 센서 업데이트 비율이 훨씬 낮기 때문에 센서 측정에 대한 걱정은 아니다. 그러나 대역폭 감소는 저역 통과 필터로 작용하고 노이즈가 시스템에 들어가는 것을 허용하지 않기 때문에 하나의 장점일 수 있다.
로드셀 인터페이스에서 또 다른 중요한 관심사는 출력 시그널 범위가 여기 전압에 의존하기 때문에, 이득 오차가 있을 수 있다는 점이다. 여기 전압의 작은 변화는 측정에서 비슷한 비율로 이득 오차를 발생시킬 수 있다. 만일 시그널 측정이 여기 전압에 대한 비율로 만들어진다면, 우리는 이를 피할 수 있다. 이는 다음과 같은 두 가지 방법으로 달성할 수 있다:

1. 우리는 개별적으로 시그널과 여기 전압을 측정하고 그런 다음 비율을 계산할 수 있다. 따라서 이득 오차를 없앨 수 있다. 그러나 이 방법은 두 시그널 간의 ADC 멀티플렉싱을 필요로 한다. 또 다른 문제는 우리가 측정하고 있는 시그널이 10 mV 범위에 있으며 여기 전압이 전압 범위에 있을 것이라는 점이다. 이는 대부분의 아날로그 시스템에서는 권장하지 않는 동적으로 변화하는 이득 설정과 ADC 매개변수를 의미하는 것이다.
2. 또 다른 두 번째 방법은 ADC 자체에 레퍼런스를 이용하는 것이다. ADC는 일반적으로 외부 레퍼런스에 연결하기 위한 레퍼런스 핀을 가지고 있다. ADC에서 이루어지는 모든 측정은 레퍼런스와 관련하여 이루어진다. 따라서 우리가 ADC에 레퍼런스로서 여기 전압이나 분리 유도체(di
vided derivative)를 제공했다면, 우리는 시그널에 대한 비례적(ratio-metric) 측정을 얻을 수 있다.

디지털 필터
지금까지 우리는 아날로그 시그널 체인에서 노이즈 및 오차 소스를 피하기 위한 몇 가지 방법을 알아봤다. 노이즈 없는 출력을 얻기 위한 최종 단계 중 하나는 노이즈를 평균에 도달시키기 위해 펌웨어 기반의 수학적 필터를 이용하는 것이다. 구현하기 쉬운 한 가지 필터는 이동 평균 필터(moving average filter)이다. 어떤 주어진 시간에 필터의 출력은 어레이에서 모든 요소의 평균이다.
이동 평균 필터는 측정 시스템에서 노이즈가 없는 보다 더 높은 비트를 달성하기 위한 가장 효과적인 필터 중 하나다. 단점은 사용되는 어레이의 깊이에 비례하는 일정한 지연이 있다는 것이다. 이것은 n-element 이동 평균 필터에서의 변화가 출력 자체를 반영하기 위해 n 사이클이 걸릴 수 있다는 것을 의미한다. 이것은 보다 큰 변화가 있고 출력이 천천히 잡히는 경우 약간 오해가 있을 수도 있다. 이러한 조건은 변화에 임계값 조건을 점검함으로써 피할 수 있다. 입력이 특정 시점에서 임계값보다 더 많이 변할 경우 전체 필터는 플러시되며 새로운 데이터는 필터와 출력으로 또한 복사된다. 따라서 더 큰 변화를 위한 대기 시간이 감소된다.